blakecmathis
Well-known member
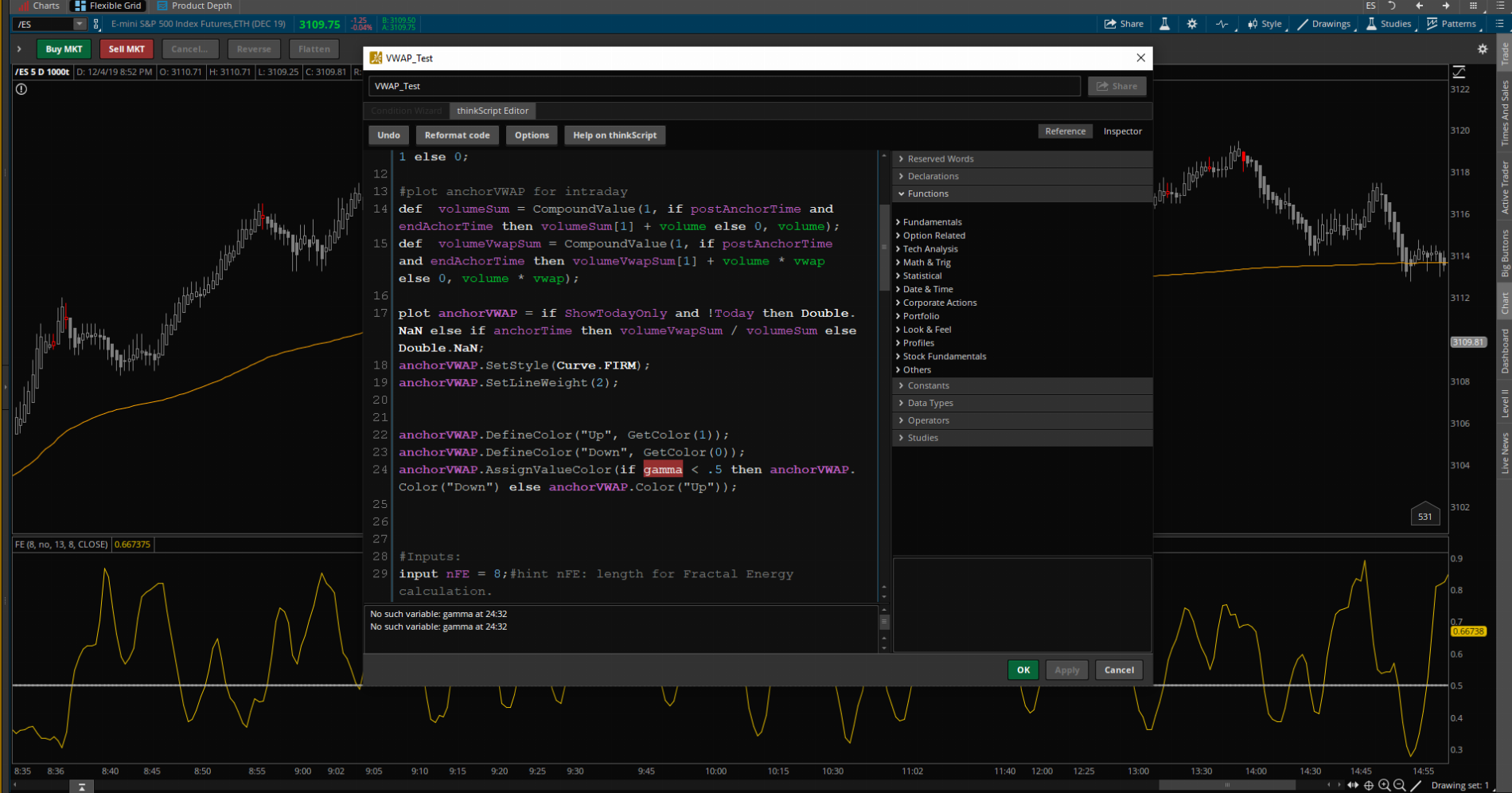
I know this sounds crazy but hear me out. I would like to color code the intraday VWAP according to Fractal Energy. When FE falls below .5, I would like the VWAP to be Color A and then Color B for all other levels. Essentially the same way a Hull MA shifts colors. I've attempted to recreate what I am searching for in the screenshot below. When FE falls below .5, VWAP changes to blue. Tried to do it myself but couldn't find a solution (I have no idea what I'm doing). I really hope this is possible. Any help is greatly appreciated
I have already merged the two here: https://tos.mx/6XSCJKd
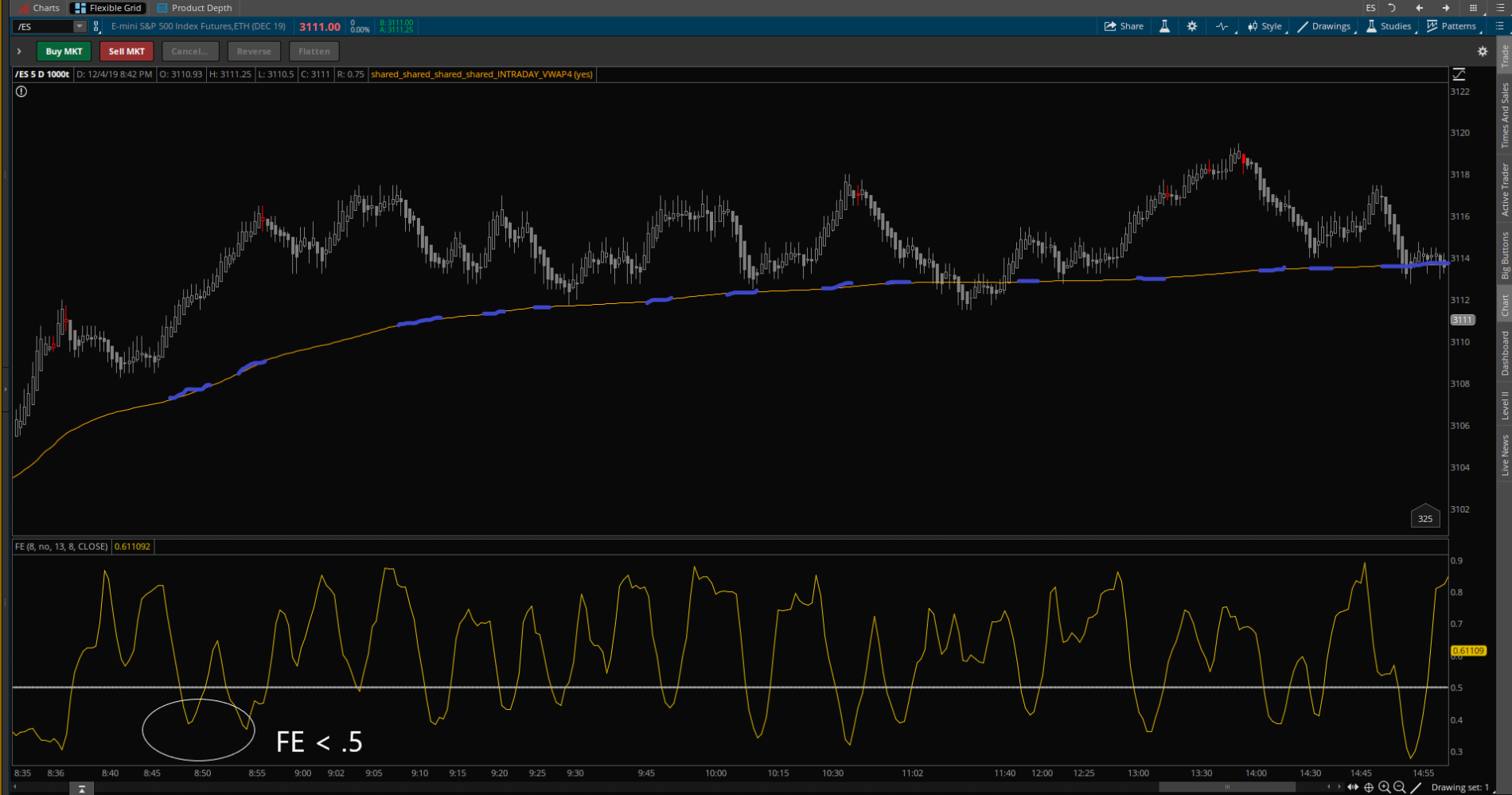
I have already merged the two here: https://tos.mx/6XSCJKd
Code:
#yakBro intraday anchoredVWAP excluding extended hours volume 2019
declare upper;
def anchorTime = 0930;
def anchorEnd = 1600;
input ShowTodayOnly = yes;
def Today = if GetDay() == GetLastDay() then 1 else 0;
def postAnchorTime = if SecondsFromTime(anchorTime) >= 0 then 1 else 0;
def endAchorTime = if SecondsTillTime(anchorEnd) >= 0 then 1 else 0;
#plot anchorVWAP for intraday
def volumeSum = CompoundValue(1, if postAnchorTime and endAchorTime then volumeSum[1] + volume else 0, volume);
def volumeVwapSum = CompoundValue(1, if postAnchorTime and endAchorTime then volumeVwapSum[1] + volume * vwap else 0, volume * vwap);
plot anchorVWAP = if ShowTodayOnly and !Today then Double.NaN else if anchorTime then volumeVwapSum / volumeSum else Double.NaN;
anchorVWAP.SetStyle(Curve.FIRM);
anchorVWAP.SetLineWeight(2);
anchorVWAP.DefineColor("Up", GetColor(1));
anchorVWAP.DefineColor("Down", GetColor(0));
anchorVWAP.AssignValueColor(if gamma < .5 then anchorVWAP.Color("Down") else anchorVWAP.Color("Up"));
#Inputs:
input nFE = 8;#hint nFE: length for Fractal Energy calculation.
input AlertOn = no;
input Glength = 13;
input betaDev = 8;
input data = close;
def w = (2 * Double.Pi / Glength);
def beta = (1 - Cos(w)) / (Power(1.414, 2.0 / betaDev) - 1 );
def alpha = (-beta + Sqrt(beta * beta + 2 * beta));
def Go = Power(alpha, 4) * open +
4 * (1 – alpha) * Go[1] – 6 * Power( 1 - alpha, 2 ) * Go[2] +
4 * Power( 1 - alpha, 3 ) * Go[3] - Power( 1 - alpha, 4 ) * Go[4];
def Gh = Power(alpha, 4) * high +
4 * (1 – alpha) * Gh[1] – 6 * Power( 1 - alpha, 2 ) * Gh[2] +
4 * Power( 1 - alpha, 3 ) * Gh[3] - Power( 1 - alpha, 4 ) * Gh[4];
def Gl = Power(alpha, 4) * low +
4 * (1 – alpha) * Gl[1] – 6 * Power( 1 - alpha, 2 ) * Gl[2] +
4 * Power( 1 - alpha, 3 ) * Gl[3] - Power( 1 - alpha, 4 ) * Gl[4];
def Gc = Power(alpha, 4) * data +
4 * (1 – alpha) * Gc[1] – 6 * Power( 1 - alpha, 2 ) * Gc[2] +
4 * Power( 1 - alpha, 3 ) * Gc[3] - Power( 1 - alpha, 4 ) * Gc[4];
# Variables:
def o;
def h;
def l;
def c;
def CU1;
def CU2;
def CU;
def CD1;
def CD2;
def CD;
def L0;
def L1;
def L2;
def L3;
# Calculations
o = (Go + Gc[1]) / 2;
h = Max(Gh, Gc[1]);
l = Min(Gl, Gc[1]);
c = (o + h + l + Gc) / 4;
def gamma = Log(Sum((Max(Gh, Gc[1]) - Min(Gl, Gc[1])), nFE) /
(Highest(Gh, nFE) - Lowest(Gl, nFE)))
/ Log(nFE);
L0 = (1 – gamma) * Gc + gamma * L0[1];
L1 = -gamma * L0 + L0[1] + gamma * L1[1];
L2 = -gamma * L1 + L1[1] + gamma * L2[1];
L3 = -gamma * L2 + L2[1] + gamma * L3[1];
if L0 >= L1
then {
CU1 = L0 - L1;
CD1 = 0;
} else {
CD1 = L1 - L0;
CU1 = 0;
}
if L1 >= L2
then {
CU2 = CU1 + L1 - L2;
CD2 = CD1;
} else {
CD2 = CD1 + L2 - L1;
CU2 = CU1;
}
if L2 >= L3
then {
CU = CU2 + L2 - L3;
CD = CD2;
} else {
CU = CU2;
CD = CD2 + L3 - L2;
}