YungTraderFromMontana
Well-known member
There is one crucial signal of the fe and hurst exponent waves I use that I can not seem to get into code. If anyone can do this it will be the next big breakthrough for my Ultimate indicator thread and the community as well as myself would greatly appreciate it.
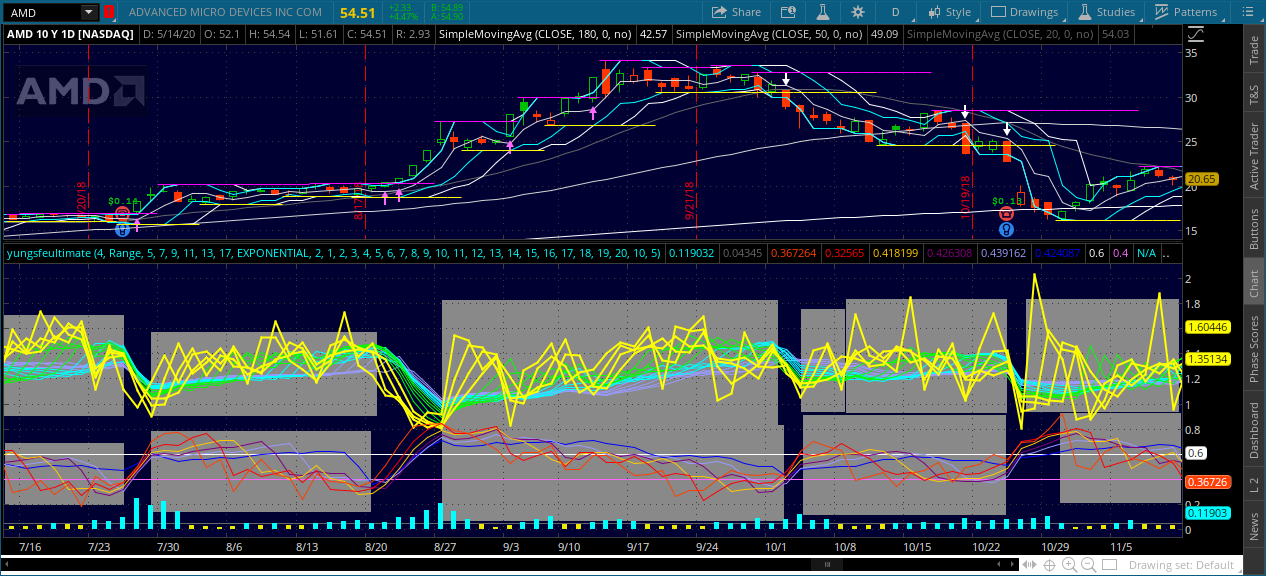
Here's the puzzle, along with the signal of these studies which is simply looking for a strong movement up or down, a second signal that can be easily seen with the eyes but difficult to translate the code is the difference between periods of seemingly random readings as compared to periods of precise readings of these indicators. Here are some examples. Remember that fe and he are non-directional. Ignore the acc/dist study at the bottom, this is somewhat of a csa I use. FE is in yellow/green/blue/purple and HE is in red/orange/yellow/purple, these studies are simply multiple lengths of the study.
In this picture I highlighted the areas I would call random and left alone the areas I would say the indicator readings are amalgamated.
Notice the different characteristics of these different states, random gaps between the lines and highly varied linear direction of the different fe lengths tell me to avoid a trade, when the lines form a synchronized sort of wave in length order with only gaps between lower lengths this tells me that the stock will trend after a breakout. These are the factors I want to be able to gauge somehow.
I'm going to put the code at the end for reference.
I really hope one of you will take on the challenge, it's certainly a difficult challenge that I have failed at many times. Although I can see the signals with my own eyes but this would save precious time when it comes to scan stocks by narrowing down the total amount of results massively. Please ask any questions if you have any.
@mashume @diazlaz @horserider @markos @BenTen
Here's the puzzle, along with the signal of these studies which is simply looking for a strong movement up or down, a second signal that can be easily seen with the eyes but difficult to translate the code is the difference between periods of seemingly random readings as compared to periods of precise readings of these indicators. Here are some examples. Remember that fe and he are non-directional. Ignore the acc/dist study at the bottom, this is somewhat of a csa I use. FE is in yellow/green/blue/purple and HE is in red/orange/yellow/purple, these studies are simply multiple lengths of the study.
In this picture I highlighted the areas I would call random and left alone the areas I would say the indicator readings are amalgamated.
Notice the different characteristics of these different states, random gaps between the lines and highly varied linear direction of the different fe lengths tell me to avoid a trade, when the lines form a synchronized sort of wave in length order with only gaps between lower lengths this tells me that the stock will trend after a breakout. These are the factors I want to be able to gauge somehow.
I'm going to put the code at the end for reference.
I really hope one of you will take on the challenge, it's certainly a difficult challenge that I have failed at many times. Although I can see the signals with my own eyes but this would save precious time when it comes to scan stocks by narrowing down the total amount of results massively. Please ask any questions if you have any.
Code:
# TheoTrade RSI in Laguerre Time Self Adjusting With Fractal Energy
# Mobius
# V03.06.15.2016
# Both Fractal Energy and RSI are plotted. RSI in cyan and FE in yellow. Look for trend exhaustion in the FE and a reversal of RSI or Price compression in FE and an RSI reversal.
declare lower;
input length69 = 4;
def factor = .869;
input mode = {default Range, ATR};
def range;
switch (mode) {
case Range:
range = Highest(high, length69) - Lowest(low, length69);
case ATR:
range = reference ATR();
}
plot RangeRatio = (range / range[length69])/20;
plot RangeFactor = factor/20;
RangeRatio.SetPaintingStrategy(PaintingStrategy.HISTOGRAM);
RangeRatio.DefineColor("Consolidation", GetColor(4));
RangeRatio.DefineColor("Non-consolidation", GetColor(1));
RangeRatio.AssignValueColor( if (RangeRatio < RangeFactor) then RangeRatio.Color("Consolidation") else RangeRatio.Color("Non-consolidation"));
RangeFactor.SetDefaultColor(GetColor(7));
input length2 = 5;
input length3 = 7;
input length4 = 9;
input length5 = 11;
input length6 = 13;
input length7 = 17;
input averageType = AverageType.EXPONENTIAL;
input lengthave =2;
def ll2 = Lowest(low, length2);
def hh2 = Highest(high, length2);
def atr2 = MovingAverage(averageType, TrueRange(high, close, low), length2);
def tmp_H2 = (Log(hh2 - ll2) - Log(atr2)) / (Log(length2));
plot H2;
if tmp_H2 > 1
then {
H2 = 1;
} else if tmp_H2 < 0 {
H2 = 0;
} else {
H2 = tmp_H2;
}
def ll3 = Lowest(low, length3);
def hh3 = Highest(high, length3);
def atr3 = MovingAverage(averageType, TrueRange(high, close, low), length3);
def tmp_H3 = (Log(hh3 - ll3) - Log(atr3)) / (Log(length3));
plot H3;
if tmp_H3 > 1
then {
H3 = 1;
} else if tmp_H3 < 0 {
H3 = 0;
} else {
H3 = tmp_H3;
}
def ll4 = Lowest(low, length4);
def hh4 = Highest(high, length4);
def atr4 = MovingAverage(averageType, TrueRange(high, close, low), length4);
def tmp_H4 = (Log(hh4 - ll4) - Log(atr4)) / (Log(length4));
plot H4;
if tmp_H4 > 1
then {
H4 = 1;
} else if tmp_H4 < 0 {
H4 = 0;
} else {
H4 = tmp_H4;
}
def ll5 = Lowest(low, length5);
def hh5 = Highest(high, length5);
def atr5 = MovingAverage(averageType, TrueRange(high, close, low), length5);
def tmp_H5 = (Log(hh5 - ll5) - Log(atr5)) / (Log(length5));
plot H5;
if tmp_H5 > 1
then {
H5 = 1;
} else if tmp_H5 < 0 {
H5 = 0;
} else {
H5 = tmp_H5;
}
def ll6 = Lowest(low, length6);
def hh6 = Highest(high, length6);
def atr6 = MovingAverage(averageType, TrueRange(high, close, low), length6);
def tmp_H6 = (Log(hh6 - ll6) - Log(atr6)) / (Log(length6));
plot H6;
if tmp_H6 > 1
then {
H6 = 1;
} else if tmp_H6 < 0 {
H6 = 0;
} else {
H6 = tmp_H6;
}
def ll7 = Lowest(low, length7);
def hh7 = Highest(high, length7);
def atr7 = MovingAverage(averageType, TrueRange(high, close, low), length7);
def tmp_H7 = (Log(hh7 - ll7) - Log(atr7)) / (Log(length7));
plot H7;
if tmp_H7 > 1
then {
H7 = 1;
} else if tmp_H7 < 0 {
H7 = 0;
} else {
H7 = tmp_H7;
}
h2.SetDefaultColor(Color.light_red);
h3.SetDefaultColor(Color.red);
h4.SetDefaultColor(Color.orange);
h5.SetDefaultColor(Color.plum);
h6.SetDefaultColor(Color.violet);
h7.SetDefaultColor(Color.blue);
plot high = .6;
plot low = .4;
#Inputs:
input nfe1 = 1;
input nfe2 = 2;
input nfe3 = 3;
input nfe4 = 4;
input nfe5 = 5;
input nfe6 = 6;
input nfe7 = 7;
input nfe8 = 8;
input nfe9 = 9;
input nfe10 = 10;
input nfe11 = 11;
input nfe12 = 12;
input nfe13 = 13;
input nfe14 = 14;
input nfe15 = 15;
input nfe16 = 16;
input nfe17 = 17;
input nfe18 = 18;
input nfe19 = 19;
input nfe20 = 20;
input length = 10;
input smoothingLength = 5;
#hint nFE: length for Fractal Energy calculation.
# Variables:
def o;
def h;
def l;
def c;
# Calculations
o = (open + close[1]) / 2;
h = Max(high, close[1]);
l = Min(low, close[1]);
c = (o + h + l + close) / 4;
# Gamma Function
script gammax {
input nFEi = 12;
def FE = Log(Sum((Max(high, close[1]) - Min(low, close[1])), nFEi) /
(Highest(high, nFEi) - Lowest(low, nFEi)))
/ Log(nFEi);
plot gamma = FE + .8;
}
plot gamma = gammax(nfe1);
gamma.SetDefaultColor(Color.CYAN);
plot gamma2 = gammax(nfe2);
gamma2.SetDefaultColor(Color.YELLOW);
gamma2.SetLineWeight(2);
plot gamma3 = gammax(nfe3);
gamma3.SetDefaultColor(Color.YELLOW);
gamma3.SetLineWeight(2);
plot gamma4 = gammax(nfe4);
gamma4.SetDefaultColor(Color.YELLOW);
gamma4.SetLineWeight(2);
plot gamma5 = gammax(nfe5);
gamma5.SetDefaultColor(Color.YELLOW);
gamma5.SetLineWeight(2);
plot gamma6 = gammax(nfe6);
gamma6.SetDefaultColor(Color.GREEN);
plot gamma7 = gammax(nfe7);
gamma7.SetDefaultColor(Color.GREEN);
plot gamma8 = gammax(nfe8);
gamma8.SetDefaultColor(Color.GREEN);
plot gamma9 = gammax(nfe9);
gamma9.SetDefaultColor(Color.GREEN);
plot gamma10 = gammax(nfe10);
gamma10.SetDefaultColor(Color.GREEN);
plot gamma11 = gammax(nfe11);
gamma11.SetDefaultColor(Color.CYAN);
plot gamma12 = gammax(nfe12);
gamma12.SetDefaultColor(Color.CYAN);
plot gamma13 = gammax(nfe13);
gamma13.SetDefaultColor(Color.CYAN);
plot gamma14 = gammax(nfe14);
gamma14.SetDefaultColor(Color.CYAN);
plot gamma15 = gammax(nfe15);
gamma15.SetDefaultColor(Color.CYAN);
plot gamma16 = gammax(nfe16);
gamma16.SetDefaultColor(Color.VIOLET);
plot gamma17 = gammax(nfe17);
gamma17.SetDefaultColor(Color.VIOLET);
plot gamma18 = gammax(nfe18);
gamma18.SetDefaultColor(Color.VIOLET);
plot gamma19 = gammax(nfe19);
gamma19.SetDefaultColor(Color.VIOLET);
plot gamma20 = gammax(nfe20);
gamma20.SetDefaultColor(Color.VIOLET);
def gammasector1 = (gamma2 + gamma3 + gamma4 + gamma5) / 4;
def gammasector2 = (gamma6 + gamma7 + gamma8 + gamma9 + gamma10) / 5;
def gammasector3 = (gamma11 + gamma12 + gamma13 + gamma14 + gamma15) / 5;
def gammasector4 = (gamma16 + gamma17 + gamma18 + gamma19 + gamma20) / 5;
def gammasectorcombo = (gammasector3 + gammasector4) / 2;
def gammasector22 = ((gammasector2 - gammasector4) *(gammasector2 - gammasector4)) * 1000;
#plot feblast = gammasector1[1] > gammasector1 and gammasector2[1] > gammasector2 and gammasectorcombo[1] > gammasectorcombo and close > trueqb2;
Last edited by a moderator: